論理的間違いの実例part2
親殺しのパラドックス
親殺しのパラドックスは有名です。これは、自分が生まれる前の過去に戻って親を殺すことが可能かどうかを考察したものです。
- 過去に戻って親を殺す
- 親が死ぬので自分は生まれない
- 自分が生まれなければ親は殺せない
- 親が死なないので自分が生まれる
- 過去に戻って親を殺す
- (以下、延々と繰り替えす)
しかし、これは、致命的な勘違いの産物です。結論から言えば、時空で考えるべき所を時々空=5次元を考えているところが間違いです。
説明のため、親殺しのパラドックスの流れを次のように定義します。
- 親が生きている最初の歴史・・・(1)
- 過去に戻って親を殺してしまった歴史・・・(2)
- 自分の消滅により親が死ななくなった歴史・・・(3)
さて、ここで問題です。次の事項を時系列順に並べてください。
| (1) | (2) | (3) | |
|---|---|---|---|
| 2000年1月1日11:59:59 | (1)の11:59:59 | (2)の11:59:59 | (3)の11:59:59 |
| 2000年1月1日12:00:00 | (1)の12:00:00 | (2)の12:00:00 | (3)の12:00:00 |
| 2000年1月1日12:00:01 | (1)の12:00:01 | (2)の12:00:01 | (3)の12:00:01 |
正解は次の通り。
- (1)の11:59:59=(2)の11:59:59=(3)の11:59:59
- (1)の12:00:00=(2)の12:00:00=(3)の12:00:00
- (1)の12:00:01=(2)の12:00:01=(3)の12:00:01
(1)も(2)も(3)も同時刻なら同時なのです。11:59:59 → 12:00:00 → 12:00:01という時間の流れは存在しても、(1) → (2) → (3)という時間の流れは存在しないわけです。言い替えると、親殺しのパラドックスに矛盾があるかのように思えるのは、通常の時間の流れの他に、存在しないはずの(1) → (2) → (3)の時間の流れを考えているからです。これが「時々空で考えている」という意味です。
絵で説明
良く分からないと言う方のために、次元を二つ落として図で示してみましょう。えっ、なぜ、二つも落とすかって?それは、絵が二次元だからです*1。だから、二次元で四次元を説明するには次元を二つ落とす必要があります。下図の上下方向が時間軸と考えてください。そして、時間の流れは下から上です。さらに、下の絵の左下から右上に書かれた一本の直線*2は固定されていて変化しないと考えてください。
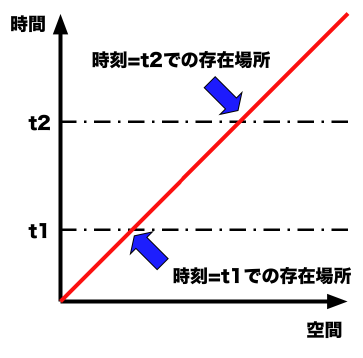
上図は、「一次元」世界で時間の流れを感じている人間にとって、一個の点が左から右に移動する様子を表しています。つまり、「二次元」的には固定でも、「一次元」的には時間経過による変化が存在するのです。
一つ次元を増やして考えてみましょう。三次元の内の一軸が時間の流れだと考えてください。この「三次元」空間上に球体が存在する場合は、次のように「二次元」的形状が時間経過と共に変化することを示しています。
- 無
- 点
- 小さな円
- 大きな円
- 小さな円
- 点
- 無
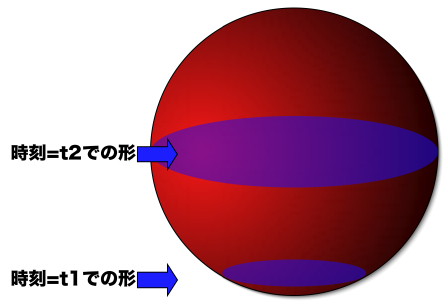
つまり、「三次元」的には固定でも、「二次元」的には時間経過による変化が存在するのです。
さらに、次元を一つ増やすとどうなるか推論してみましょう。
- 次元を二つ落とした説明では、「二次元」的には固定でも「一次元」的には時間経過による変化が存在する
- 次元を一つ落とした説明では、「三次元」的には固定でも「二次元」的には時間経過による変化が存在する
- よって、元通りの状態では、四次元的には固定でも三次元的には時間経過による変化が存在するらしい
と言えることが分かるでしょうか。
このように、固定した形が既に時間の流れを示しているのだから、さらにその形が変化すれば、最初の時間の流れとは直交した別の時間の流れが生じることを意味します。 これは、時間軸(time axisであってtime lineの意味ではない)が二つ=五次元となることを意味します。 親殺しのパラドックスにおいて、未来や過去が変わってしまうことは、四次元的形状の変化であり、これはまさに五次元で物を考えていることです。
反復法
(1) → (2) → (3)は時間の流れではなく、思考の流れに過ぎません。そして、それは、連立方程式を解く時の 反復法(Wikipedia:反復法_(数値計算)の方が分かり易いかな?具体的にはWikipedia:ガウス=ザイデル法やWikipedia:ヤコビ法などがあります。)と似た考え方です。
ある程度以上、未知数が多い連立方程式では、真面目に解くと時間がかかりすぎます。そこで、考え出されたのが反復法です。やり方を簡単に説明すると次の通り。
- 最初に、求める未知数全てに適当な値=仮の解を入れる
- その値を元に式の誤差を求める
- 式の誤差を元に未知数の値を修正する
- 修正した値を新たな仮の解として計算を繰り返す
- 式の誤差が一定値以下になったら計算を打ち切る
そして、この方法には次のような欠点があります。
- 計算誤差がある程度生じる
- 初期値が不適切だと永遠に計算が終わらない
- 反復法に向かない方程式もある
親殺しのパラドックスは、まさに、初期値が不適切だったために永遠に計算が終わらない状態そのものです。計画の成功が遂行不能状態を生み出すという完全に相反する初期値、つまり、完全にあり得ない初期値を入れるから解が求まらないだけです。逆に言えば、少々矛盾する程度の現象を初期値として入れておけば、解が求まる可能性があるのです。そうして求まり得る解の分かりやすい例として、物理学者によるタイムパラドックス分析では「自分殺しのパラドックス」が紹介されています。
尚、計算途中の仮の解に現実的意味を求めても意味はありません。最終的に求まった解は実在する解です。しかし、計算途中の値は、実在しない架空の値に過ぎず、現実的意味はありません。まして、解が求まらない場合の計算途中になど、現実的意味が存在するわけがないのです。現実的な意味のない物に現実的意味を考えようとするから、訳が分からなくなるわけです。ありもしない幻を追いかけても得る物はありません。ここは、潔く、考えるのを止めるのが正解です。いや、アプローチ方法を変える(=初めから解に近い初期値を入れる)と言った方が正確ですね。
架空の疑問
Ever17やRemember11には、歴史を維持するための行動が随所に見られます。では、その維持すべき歴史を作ったのは誰でしょうか。結論を言えば、それは擬似問題であり、答えはありません。誰かの意志に従って歴史が作られなければならないと思うから疑問が生じるのであって、なるようになったと考えれば疑問は全く生じません。
先に述べたとおり、親殺しのパラドックスがパラドックスとなるのは、計画と実績の差を見逃しているからです。何事も計画通りに100%成功する・・・方が変でしょう。だから、計画と実績には何らかの差が生じるのは当たり前です。差は大小様々な値を採り得ます。極端な場合、計画と実績が全く違う物になる可能性もあります。にもかかわらず、差を0と決め付けるからパラドックスに陥るわけです。
例えば、貴方がAさんを殺そうとすると、それは、どんな結果を生むでしょうか。
- Aさんが死ぬ
- Aさんが死なずに、Bさんが死ぬ
- Aさんが死なずに、貴方が死ぬ
もっと予想外の事態になる可能性*3もあります。逆に言えば、Aさんが死んだという結果からは、Aさんへの誰かの殺意があったかどうかまでは分かりません。言い替えると、Aさんへの殺意が無くとも、Aさんが死ぬことがあります。
これと同様、タイム・ループの中の維持すべき歴史についても、それを作ろうとした誰かの意思は必要ありません。しいて言えば、その歴史を作ったのは方程式の係数です。係数が別の値であれば、違う歴史になったかも知れません。その係数には誰かの意思が働いていますから、維持すべき歴史は、誰かの意志が間接的に働いているとは言えます。しかし、直接的にその歴史を作ろうとした意思は必要ありません。計画と実績の差を柔軟に考えれば良いのです。風が吹けば桶屋が儲かるように、誰かの意思が巡り巡って予想外の歴史を作り出したと考えれば良いのです。その意思がどのように歴史に影響を及ぼすか、その法則性は「方程式による」としか言えません。言い替えれば、方程式に頼らない単純な法則性は存在しなくて当たり前なのです。存在しない法則性を見いだそうとするからパラドックスに陥るのです。
誰の意志も働かなくても、歴史は発生します。もし、歴史に意思が必須であるなら、生物が生まれることはなかったはずです。なぜなら、生物誕生前には誰の意思も存在しないからです。それなのに、生物誕生という歴史が発生しています。ということは、歴史に意思は必須でないということです。そのことを偶然や神の意志で納得できるなら、維持すべき歴史の発生も偶然や神の意志で納得できるはずです。誰も意図しなくても、物事はなるようになるのです。
ただし、それまでの歴史に存在しなかった極めて複雑な存在が方程式の解となることは偶然にしては出来過ぎています。また、特定の解を導くように係数値を選別する働きがなければ、その解が得られることに必然性は認められない。そうしたことは現実に起こることは、まず、ないと言えます。しかし、物語の条件にも書いたとおり、作り話に厳密な科学考証は不要です。いや、あまり厳密な科学考証を追い求めすぎると話を作ることが困難なので、作り話における科学考証はホドホドに止めておくべきでしょう。偶然でも説明不能な現象が起きては荒唐無稽すぎるとしても、偶然で片付くことであるなら十分に許容範囲なはずです。
Keyword(s):[共通]
References:[Remember11考察] [並行世界におけるタイムパラドックス] [Remember11真相] [Ever17考察] [12RIVEN考察] [考察の基本原則]